多層パーセプトロンとは？概要とPythonによる実装をチェック！

こんにちは！侍エンジニアです。この記事はディープラーニングを基礎の基礎から理解していくシリーズの2本目です。

一本目はこちら↓

単純パーセプトロンの仕組みとPythonによる実装をチェック

更新日：2024年4月29日

この記事では多層パーセプトロンについて紹介します。

多層パーセプトロンは一本目の記事で紹介した単純パーセプトロンを発展させて、複数のパーセプトロンを組み合わせたアルゴリズムです。

この多層パーセプトロンがどういうものか、何ができてどうやってPythonで実装するのかに注目して解説してきます！

多層パーセプトロンとは

概要

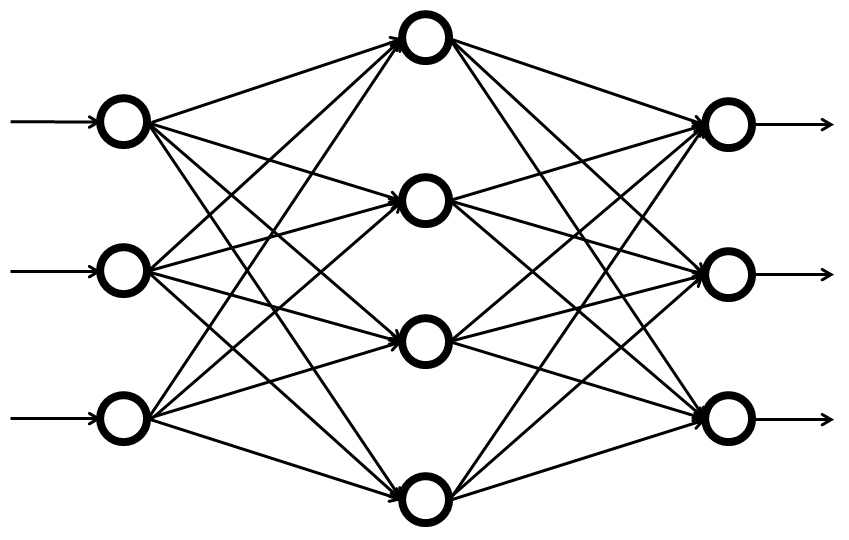
多層パーセプトロンとは、複数の単純パーセプトロンを組み合わせて層を深くしたアルゴリズムです。

[多層パーセプトロンのイメージ図: http://nkdkccmbr.hateblo.jp/entry/2016/10/06/222245 より]

単純パーセプトロン単体だと、一本の直線で分離できない問題に対応できませんでした。

多層パーセプトロンでは、複数のパーセプトロンを組み合わせて使うため、この問題を解決できます！

使いみち

単純パーセプトロンの記事では、ANDゲートを再現するプログラムを実装しました。

多層パーセプトロンでもこの流れを組んで論理演算を再現します。

単純パーセプトロンの記事の最後で、XOR（排他的論理和）という線形分離できない問題について紹介しましたね。

ですがXORは、AND、NAND、ORの三種類の論理ゲートを組み合わせることで、再現が可能です。

このように複数の単純パーセプトロンを組み合わせて解けるような問題に多層パーセプトロンは活躍します。

多層パーセプトロンの実装

この記事では、多層パーセプトロンの解説で多分もっともよく出てくる問題である「XORゲートの実装」を行います。

XORとは

まずはライブラリをimportしましょう。

import pandas as pd
import numpy as np
import matplotlib
import matplotlib.pyplot as plt

XORの論理値表を見てみましょう。

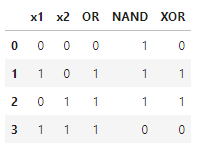
XORはx1とx2が同じ値のとき0,異なる値のとき1を返す論理演算です。

これを再現するには、以下のような論理回路を用意します。

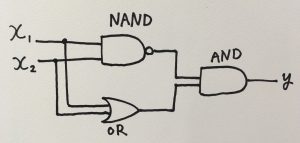
ここに出てきたAND、OR、NANDは単純パーセプトロンのみで再現可能です。

つまり、これらを組み合わせることで、XORが再現できることがわかります。

実装

前回の記事でANDゲートを実装しました。

AND関数のパラメータを変えるだけで、ORゲートとNANDゲートの実装ができます。

def AND_gate(x1,x2):
    b = -0.7
    w = np.array([0.5,0.5]) # w1, w2 = 0.5,0.5
    x = np.array([x1,x2])
    
    tmp = np.sum(w*x)+b
    if tmp <= 0.0:
        y = 0
    else:
        y = 1    
    return y

def OR_gate(x1,x2):
    b = -0.2 
    w = np.array([0.5,0.5]) # w1, w2 = 0.5,0.5
    x = np.array([x1,x2])
    
    tmp = np.sum(w*x)+b
    if tmp <= 0.0:
        y = 0
    else:
        y = 1    
    return y

def NAND_gate(x1,x2):
    b = 0.7 
    w = np.array([-0.5,-0.5]) # w1, w2 = 0.5,0.5
    x = np.array([x1,x2])
    
    tmp = np.sum(w*x)+b
    if tmp <= 0.0:
        y = 0
    else:
        y = 1    
    return y

ここではNumpyを使って簡単に３つの論理ゲートを書きました。

さて、これらを使ってXORゲートを実装します。

def XOR_gate(x1,x2):
    a = OR_gate(x1,x2)
    b = NAND_gate(x1,x2)
    y = AND_gate(a, b)
    return y

このXOR_gate関数で目的の「XORゲートの動きをする多層パーセプトロン」が実装できました。

そしてこのXOR_gate関数の出力値をチェックしてみます。

print(XOR_gate(0,0))
print(XOR_gate(1,0))
print(XOR_gate(0,1))
print(XOR_gate(1,1))

# 出力結果
0
1
1
0

結果を見ると、正しい解答が出せていることがわかります。

この記事で紹介した多層パーセプトロンの問題点

この記事で紹介した多層パーセプトロンは、結合重みやバイアスなどのパラメータを決め打ちで使っています。

XOR問題のような簡単な問題ならば、それも可能です。

ですが実際には、画像認識や音声認識などのより難しい問題にニューラルネットワークを使いたいはず。

このような問題に適用したいならば、この記事や単純パーセプトロンの記事で紹介したような「手作業でパラメータを決める方法」は不適切です。

さて、実際に広く使われているニューラルネットワークでは、データと正解ラベルからパラメータを自動的に学習させます。

多分こちらのほうが「人工知能」という言葉のイメージに近いんじゃないでしょうか。

このパラメータの自動学習について、また別の記事で紹介します。

まとめ

この記事では多層パーセプトロンについて紹介しました。

パーセプトロンのすごいところは、これを組み合わせて多層化することで、表現力を上げることができる点ですね。

また、これ以外にも、活性化関数（これについても別記事で解説します）を変えるなどの方法で更に性能を変化させる事ができます。

本当にいろいろなことに応用できるアルゴリズムなので、是非試してみてください！