こんにちは!インストラクターのフクロウです。
中学高校で習った対数、皆さん覚えているでしょうか。行列計算を得意とするNumPyにも、もちろん対数関数の実装があります。この記事では、NumPyに実装された4つの対数関数について紹介していきますよ!
実は機械学習の実装において無くてはならない機能である対数、NumPyの勉強と一緒に思い出してみませんか?
logの使い方
※この記事のコードは、jupyter notebookやjuputer labを使って書かれています。
コードを試すときは是非これらを使ってみてください。
まずはライブラリをimportしましょう。
# コード In [1]: import numpy as np import matplotlib.pyplot as plt
さて、numpyには対数に関する関数が4つあります。
- np.log(a)
- 底をeとするaの対数
- np.log2(a)
- 底を2とするaの対数
- np.log10(a)
- 底を10とするaの対数
- np.log1p(a)
- 底をeとするa+1の対数
それぞれを数式っぽく書いてみると下のようになります。
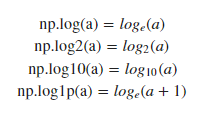
基本的には対数の底が変わったものが収められていますね。
NumPyを使ってこれらの対数関数を試してみましょう。まずはサンプル配列を用意します。
# コード In [2]: a = np.linspace(1,100,1000)
この配列に対して、先程紹介した4つの対数関数を使ってみます。
# コード In [3]: log_a = np.log(a) log2_a = np.log2(a) log10_a = np.log10(a) log1p_a = np.log1p(a)
np.log系の関数は、他のNumPyの一般的な関数と同様に、配列の要素全てに対して作用します。中身とそのグラフを見てみましょう。
# コード In [4]:
print("original")
print(a[:10])
print("n log")
print(log_a[:10])
print("n log2")
print(log2_a[:10])
print("n log10")
print(log10_a[:10])
print("n log1p")
print(log1p_a[:10])
# 出力結果 [4]: original [1. 1.0990991 1.1981982 1.2972973 1.3963964 1.4954955 1.59459459 1.69369369 1.79279279 1.89189189] log [0. 0.09449084 0.18081893 0.2602831 0.33389492 0.40245759 0.46661953 0.52691176 0.58377462 0.63757733] log2 [0. 0.13632147 0.26086657 0.37550914 0.48170854 0.58062356 0.67318968 0.76017299 0.84220875 0.91982965] log10 [0. 0.04103685 0.07852866 0.11303951 0.14500872 0.17478511 0.20265029 0.22883487 0.2535301 0.27689632] log1p [0.69314718 0.74150825 0.78763802 0.83173334 0.87396611 0.9144873 0.95343028 0.99091337 1.0270421 1.06191092]
# コード In [5]: fig = plt.figure(figsize=(10,10)) plt.plot(log_a, label="log_e") plt.plot(log2_a, label="log_2") plt.plot(log10_a, label="log_10") plt.plot(log1p_a, label="log_1p") plt.legend()
# 出力結果 Out [5]:
底の違いによって結構値が変わることがわかりますね。それに対して、logとlog1pの差はかなり小さいようです。
0以下の値と対数の関係
さて、NumPyの対数関数実装に限らず、対数は0以下の計算ができません。0の値を入れると-inf, マイナスの値を入れると計算できないのでNaNになってしまいます。
# コード In [6]: np.log(np.linspace(-10,0,10))
# 出力結果 [6]: /root/anaconda3/lib/python3.6/site-packages/ipykernel_launcher.py:1: RuntimeWarning: divide by zero encountered in log """Entry point for launching an IPython kernel. /root/anaconda3/lib/python3.6/site-packages/ipykernel_launcher.py:1: RuntimeWarning: invalid value encountered in log """Entry point for launching an IPython kernel. array([ nan, nan, nan, nan, nan, nan, nan, nan, nan, -inf])
これに対して、log1pを使えば0でも計算できます。※log(0+1)となるので。
# コード In [7]: np.log1p(0)
# 出力結果 Out [7]: 0.0
# コード In [8]: np.log1p(-1)
# 出力結果 [8]: /root/anaconda3/lib/python3.6/site-packages/ipykernel_launcher.py:1: RuntimeWarning: divide by zero encountered in log1p """Entry point for launching an IPython kernel. -inf
0を含んだ正の数を扱う場面は多いので、log1pの使い所は以外にありそうですね。
また、冒頭でも書きましたが、機械学習では対数を使う場合が多いです。例えば確率を扱う場合、確率の値は浮動小数点数になります。
そのまま確率同士を掛け算すると、アンダーフローがおこって計算がうまくできない場合があります。そんな時、対数に直してから足し算をすれば、アンダーフローの危険性を小さくする事ができます!(値のスケール感をもとに戻したい場合は、計算結果をexp関数に入れてあげればいいですね。)
また、比較したい全ての値を対数にしても、大小関係は変わらないので、上記以外の様々な場所で対数は大活躍します。
まとめ
この記事では、NumPyの対数関数実装について紹介しました。
対数を使うことで、コンピュータでの計算を安全にしたり、計算を簡単にすることができます。分野によって底が変わることが多々ありますが、NumPyならば基本的なものは全て抑えているので安心です。
是非この記事で、np.logなどの対数を計算する関数の使いかたを覚えて、機械学習や科学計算の実装に役立ててくださいね!









